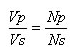Digital system is a system that serves to measure a value , or the amount of
which is fixed , or irregular in discrete form . be a digit or digits digits
digits . Usually before learning more about digital systems , first you would
have to learn the name of Numbers System . The number system has four types
namely Binary , Octal , Decimal , hexadecimal .
Biner
Binary is a number
-based system of two , and only had two pieces of symbols , 0 and 1. The modern
binary number system was discovered by Gottfried Wilhelm Leibniz in the 17th
century . The number system is the basis of all digital -based number system .
In the writing is usually written as follows 1010012 , 10012 , 10102 , etc .
Octal
Octal
is a numbers -based system of eight and had eight different symbols (
0,1,2,3,4,5,6,7 ) . In the writing is usually written as follows 23 078 , 23
558 , 1028 , etc .
Decimal
Decimal
is a number -based system of ten and has 10 different symbols (
0,1,2,3,4,5,6,7,8,9 ) . The decimal number system commonly used by humans in
everyday life .
Hexadecimal
Hexadecimal
is a numbers -based system 16 and has 16 different symbols ( 0,1,2,3,4,5,6,7,8,9
, A, B , C , D , E , F ) . In the writing is usually written as follows 2D8616
, 12DA16 , FA16 , etc .
Conversion Number
Conversion
Number is used to change a number of a system of numbers into numbers in a
number system to another.
Binary
Binary to Decimal
How to transform into
a binary number Decimal number by multiplying 2n where n is a number that
starts from the position of the numbers 0 and counted from behind .
Example
: 1100012 converted into Decimal numbers
1100012
= ( 1 x 25 ) + ( 1 x 24 ) + ( 0 x 23 ) + ( 0 x 22 ) + ( 0 x 21 ) + ( 1 x 20 )
=
32 + 16 + 0 + 0 + 0 + 1
=
49
Thus
, 110 012 = 49
Binary To Octal
How
to change the binary number into octal numbers by taking a three -digit number
from the right .
Example
: 111100110012 be converted into octal numbers
11
110 011 001 = 112 = 21 + 20 = 38
=
1102 = 22 + 21 = 68
=
0112 = 21 + 20 = 38
=
0012 = 20 = 18
So
, 111100110012 = 36 318
Binary to Hexadecimal
How
to change the binary into hexadecimal by taking four digit number from the
right .
Example
: 01001111010111002 converted to hexadecimal
0100
1111 0101 1100 = 01002 = 22 = 416
=
11112 = 23 + 22 + 21 + 20 = 15 - F16
=
01012 = 22 + 20 = 516
=
11002 = 23 + 22 = 12 - C16
So
01001111010111002 = 4F5C16
Octal
Octal To Binary
How
to transform numbers into Binary Octal , is to make one by one the numbers
Octal numbers into binary numbers first, then united . For Octal numbers must
have a 3 -digit binary number , so that if it produces less than 3 digits of
eating in front of added numbers 0
Example
: 2618 is converted into a binary number
261
= 28 = 0102
=
68 = 1102
=
18 = 0012
So , in 2618 =
0,101,100,012 .
Oktal To Decimal
How to transform into
a number Octal Decimal numbers by changing the number Octal , Binary numbers
must first become new we change into Decimal numbers .
Example
: 2618 is converted into Decimal numbers Step 1 : change the number to Binary
261 = 28 = 0102 = 68 = 1102 = 18 = 0012 So , in 2618 = 0,101,100,012 Step 2 :
turning numbers into Decimal Binary 0101100012 = ( 0 x 28 ) + ( 1 x 27 ) + ( 0
x 26 ) + ( 1 x 25 ) + ( 1 x 24 ) + ( 0 x 23 ) + ( 0 x 22 ) + ( 0 x 21 ) + ( 1 x
20 ) = 128 + 0 + 0 + 32 + 16 + 0 + 0 + 0 + 1 = 177 So , 2618 = 177
Okta To Hexadecimal
How
to change into hexadecimal numbers Octal numbers Octal by changing into binary
numbers first before we change into Decimal numbers . Then we change again into
hexadecimal .
Example
: 2618 is converted to hexadecimal
Step
1 : change the number to Binary
261
= 28 = 0102
=
68 = 1102
=
18 = 0012
So
, in 2618 = 0,101,100,012
Step
2 : turning numbers into Decimal Binary 0101100012 = ( 0 x 28 ) + ( 1 x 27 ) +
( 0 x 26 ) + ( 1 x 25 ) + ( 1 x 24 ) + ( 0 x 23 ) + ( 0 x 22 ) + ( 0 x 21 ) + (
1 x 20 ) = 128 + 0 + 0 + 32 + 16 + 0 + 0 + 0 + 1 = 177
Step
3 : turning numbers into hexadecimal Decimal 177 us for the 16-117 : 16 = 11
remainder 1 11 : 16 = 0 remainder 11 - B Reading from the bottom then becomes
B1 So 2618 = B116
Decimal
Decimal To Binary
How
to change the Decimal numbers into Binary , Decimal is to divide the number by
2 and write the rest from the bottom to the top .
Example
: 25 is converted into binary numbers
25
: 2 = 12 remainder 1
12
: 2 = 6 remainder 0
6
: 2 = 3 remainder 0
3
: 2 = 1 remainder 1
1
: 2 = 0 remainder 1
then
written 11001
So
25 = 110 012
Decimal To Octal
How
to change into Octal Decimal numbers , namely by dividing Decimal numbers with
the numbers 8 and write the rest from the bottom to the top .
Example
: 80 is converted into numbers Octal 80 : 8 = 10 remainder 0 10 : 8 = 1 the
remaining 2 1 : 8 = 0 remainder 1 then written 120 So 80 = 1208
Decimal To Hexadecimal
How
to change the Decimal numbers into hexadecimal , namely by dividing Decimal
numbers with the numbers 16 and write the rest from the bottom to the top .
Example
: 275 is converted to hexadecimal 275 : 16 = 17 remaining 3 17 : 16 = 1
remainder 1 1 : 16 = 0 remainder 1 then written 113 So 275 = 11316
Hexadecimal
Hexadecimal To Binary
How
to change the hexadecimal into binary , by making one by one hexadecimal
numbers into binary numbers first, then united . For hexadecimal numbers must
have a 4 digit binary , so if only produces less than 4 digits of eating in
front of added numbers 0 .
Example
: 4DA216 converted into binary numbers 4DA2 = 416 = 01002 = D16 = 11012 = A16 =
10102 = 216 = 00102 So 4DA216 = 01001101101000102
HExadecimal To Octal
How to change into
hexadecimal numbers Octal , is to mngubah hexadecimal numbers Decimal becomes
first, we change into octal numbers .
Example
: 3C216 converted into numbers Octal Step 1 : Change the hexadecimal be Decimal
3C216 = ( 3 x 162 ) + ( C ( 12 ) x 161 ) + ( 2 x 160 ) = 768 + 192 + 2 = 962
Step
2 : Change the Decimal numbers into Octal
962
: 8 = 120 remaining 2
120
: 8 = 15 remainder 0
15
: 8 = 1 remaining 7
1
: 8 = 0 remainder 1
it
was written in 1702
So
3C216 = 17028
Hexadecimal To decimal
How to change a binary
number to decimal, is to multiply 16N , where n is a number that starts from
the position of the numbers 0 and counted from behind .
Example
: 3C216 converted into Decimal numbers 3C216 = ( 3 x 162 ) + ( C ( 12 ) x 161 )
+ ( 2 x 160 ) = 768 + 192 + 2 = 962 So 3C216 = 962